Talk:Contradiction
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: |
|||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
Gödel Gone[edit]
I don't think that this belongs in the article:
"Misc You can't know that correct, formal reasoning will lead to consistent conclusions. This is implied in Gödel's second incompleteness theorem. This theorem says that in any system of reasoning that is powerful enough to define the numbers 1, 2, 3, ..., you cannot prove from that system that the same system will not lead to contradiction. Thus, even if you use formal rules that appear sound, it is impossible to actually prove, within that same system (or any system that is as strong - the result of Gentzen's theorem), that they will not lead to contradiction. Note that the system may still be consistent, but you may only rely on faith, intuition, and the empirical evidence stating that no such contradictions have yet been shown in such systems."
Predicate logic is not "powerful enough" to define the numbers 1, 2, 3... and therefore Godel doesn't apply to it. Furthermore the claim that "you may only rely on faith, intuition..." in logic is unsupported editorializing. The fact one cannot prove some logical system to be correct doesn't imply that one cannot know that the system is correct. Knowledge and proof are two different philosophical concepts.
To whoever added this: wikipedia is not your personal playground. There are rules against including your own original research, especially without a citation. Therefore I'm removing it. --207.252.227.7 20:53, 24 May 2005 (UTC)
German Gone[edit]
I'm removing the following German bit that was just added:
- "A ist nicht A" darstellt einen einfachen Widerspruch. Obwohl man nicht ehrlich festhalten kann, dass ein Widerspruch wahr sei, kann man trotztdem den Widerspruch als etwas Schoenes ergreifen.
Unless the following Babelfish translation is altogether inaccurate, then this doesn't add anything new. And adding nothing new in another language doesn't help anyone.
- "A is not A" represents a simple contradiction. Although one cannot hold honestly that a contradiction is true, one can seize defy-defying that the contradiction as something beautiful.
--Ryguasu 16:27 Apr 20, 2003 (UTC)
Helpful Suggestion[edit]
I take it doublethink would be difficult to place in the article. Though blackwhite might fit
article cleanup[edit]
this page seems to need cleanup by someone better versed in logic than I; it's full of little s(n)ide comments that detract from the page itself (and what's with all the bare question marks?). These seem like disagreements about the article that belong here on the talk page.
- It’s still not very good, but are there specific issues left for which the current cleanup tag should remain? —xyzzyn 21:55, 12 June 2006 (UTC)
- "In dialectics" appears to be way out of place. This article should discuss contradiction as an abstract (as in the logic section). It shouldn't get into specifics. Anyone could name any number of specific contradictions on any number of topics. Why is dialectics special? Well, it's not. Recommendation is that the "In dialectics" be removed without replacement. Fcsuper 00:46, 7 March 2007 (UTC)
- Dialectics (especially the Marx-Engels version) has been of the most significant philosophical concepts of the last two centuries in terms of impact outside philosophy and contradiction is a central concept. It’s not very well explained in the article (and, really, deserves a separate article, should anybody have the time and knowledge to write one), but it should be mentioned. —xyzzyn 14:12, 7 March 2007 (UTC)
A paradox involving contradiction -- discarded?[edit]
Luckily, I have once glanced at this article and noticed that there was a proof to the famous `theorem', which claims that any statement can be derived from a contradiction. Since that, I was looking for this proof and could not find it. Thinking that the Contradiction article is a proper place for it, I have found the proof in the history. My research has shown that the paradox explanation is unique in the Internet. Nevertheless, the regarding section was replaced by a reference to some unintelligible Coherentism. Why was such unique material removed? I want it back. --Javalenok 22:15, 3 January 2007 (UTC)
BTW, contradiction implies false and "A false statement implies anything" and its logical equivalent, "Anything implies a true statement. --Javalenok 20:51, 13 January 2007 (UTC)
- Um, what? That’s not much of a theorem. It’s usually trivial (and sometimes even the definition). Try any undergraduate textbook on logic. The diff you have provided only moves a bracket, so I have no idea to what exactly you are referring. —xyzzyn 21:52, 13 January 2007 (UTC)
- Excuse me for the confusion. Now it refers exactly to the entertaining proof of "anything from contradiction", which was removed later. I want to know why the community does not want to see it? --Javalenok 16:27, 14 January 2007 (UTC)
- Well, the example given there was quite loaded; that distracts and is therefore bad. What was described as a paradox isn’t (we really don’t need to go ‘Oh, that’s odd!’ at every fact that is not entirely intuitive). The proof consists of a look in the truth table for →. We currently assert as much in the article, but I can add it explicitely, if you wish. (The other proof is longer without adding anything interesting.) —xyzzyn 17:06, 14 January 2007 (UTC)
- I strongly beleive that the fact that controvertial theories can ground anything, enforced by the logical proof, is worth mentioning. --Javalenok 17:29, 14 January 2007 (UTC)
- That’s contradictory theories, and it’s already mentioned. I’ve added a reason. —xyzzyn 18:03, 14 January 2007 (UTC)
- A (formal) proof is much better reason, IMO, than any expert's statement. Furthermore, the definition of contradictin in the sentence preceding your reason states that contradiction=false (iff). Therefore, your reason makes no sense. Why cannot wikipedia have the proof? --Javalenok 15:38, 15 January 2007 (UTC)
- Formal proofs are good where something must be proven, but overkill for an encyclopaedia article that is not about formal proofs. By the way, why does my reason make no sense? (We can have the proof… if there’s a good place with enough context to put it.) —xyzzyn 16:10, 15 January 2007 (UTC)
- Because the ones who know that 'false' implies anything also know that 'contradiction' implies anything. --Javalenok 16:29, 15 January 2007 (UTC)
- A (formal) proof is much better reason, IMO, than any expert's statement. Furthermore, the definition of contradictin in the sentence preceding your reason states that contradiction=false (iff). Therefore, your reason makes no sense. Why cannot wikipedia have the proof? --Javalenok 15:38, 15 January 2007 (UTC)
- That’s contradictory theories, and it’s already mentioned. I’ve added a reason. —xyzzyn 18:03, 14 January 2007 (UTC)
- Excuse me for the confusion. Now it refers exactly to the entertaining proof of "anything from contradiction", which was removed later. I want to know why the community does not want to see it? --Javalenok 16:27, 14 January 2007 (UTC)
Say what?[edit]
Why is this article tagged as {{contradiction}}? Or is that some kind of a joke? --Stratadrake 22:00, 8 January 2007 (UTC)
- I guess so. [1] JackLumber. 22:14, 11 January 2007 (UTC)
Notation first?[edit]
I think the the section titled "Symbolic representation" should be the first body paragraph, rather than having two sections use the ⊥ symbol without explanation. - Callowschoolboy 17:03, 11 July 2007 (UTC)
Jargon[edit]
Can someone, ANYONE, clean this up? 63.215.29.113 23:56, 11 September 2007 (UTC)
WikiProject class rating[edit]
This article was automatically assessed because at least one WikiProject had rated the article as stub, and the rating on other projects was brought up to Stub class. BetacommandBot 03:52, 10 November 2007 (UTC)
A Question[edit]
Imagine the following universe:
- "Moment X"=TRUE; "There's light"=FALSE; "The fact is empirically true"=TRUE
- "Moment X"=FALSE; "There's light"=TRUE; "The fact is empirically true"=TRUE
- Any other combination between "Moment X" and "There's light"...; "The fact is empirically true"=FALSE
Considering this universe, what sense makes the expression ("There's light" AND NOT("There's light"))?
(Also, Problem of future contingents). --Faustnh (talk) 22:13, 20 March 2009 (UTC)
So not true[edit]
"In dialectical materialism, contradiction, as derived by Karl Marx from Hegelianism, usually refers to an opposition of social forces." I suppose the author hasn't heard about Engels's book, the "Dialectics of nature"? —Preceding unsigned comment added by 79.164.101.91 (talk) 22:10, 30 April 2009 (UTC)
If it's not a contradiction, what is it?[edit]
If you don't have a contradiction, then what do you have? I remember studying this but I forget. It can be complimentary? It's a box of four different sillogisms or something? Can we please include this in the article? --CyclePat (talk) 16:15, 26 June 2009 (UTC)
- It's satisfiable, if the logic is complete. I've added the equivalence of contradictoriness and unsatisfiability for suhc logics to the article. — Charles Stewart (talk) 19:31, 26 June 2009 (UTC)
Reversion of long footnote, etc[edit]
Yeah, you're right. The quote is not self-evident and does need some explanation. Actually it is quite relevant to the article -- it represents the classical justification for the notion of contradiction: it demonstrates Socrates' paradox used to rebutt the Sophists' argument that no notion of "contradiction" exists, that is, one can only assert truth and of falsity one must be silent. Both Plato and Aristotle were beset upon by the Sophists; both that quote and the quote(s) from which the Law of (non-)contradiction derives (I have it too, oodles of it) were rebuttals to the Sophist arguments.
The question of course is, how do we incorporate this into the article? I suppose I can create the (beginnings of) a history section. A brief mention of Plato isn't good enough. I can certainly paraphrase the quote, but the original is rather funny and clever (just awfully long).
It turns out the notion of "contradiction" is quite sophisticated. What we take for granted colloquially we cannot take for granted when we are constructing proofs of consistency. I was working on an addition to the article that pulls in both Post's 1930 proof of the consistency of the propositional logic of PM as well as Nagel and Newman's version of it.
- A paraphrase and summary of the Plato quote would be useful. I believe this could merit a paragraph in the history section, but no more than a sentence in the lead. In any case, I do not believe that such a long quote fits in an article of this brief length, nor really even in a longer article where an encyclopedia should summarize and paraphrase rather than perform actual exegesis of primary sources. LotLE×talk 22:55, 4 November 2009 (UTC)
- I appreciate the input.This is why we have editors. There have been debates re use of "primary sources" (I'm a proponent), but I suppose this one was over the top. It certainly needed an explanation. I'll figure something out (I have to go away and mull a while). I wish there were more secondary (or primary) sources but I haven't encountered any re "contradiction", and I've been through quite a few, e.g. see User:Wvbailey/Law of Excluded Middle. Also, if you or others can comment on the following, have at it... . Thanks, Bill Wvbailey (talk) 00:49, 5 November 2009 (UTC)
Someone please vet this -- Possible addition: Problem of Contradiction in consistency proofs[edit]
[Whether this goes here or in the Consistency article is open to debate.]
A Consistency proof requires (i) an axiomatic system (ii) a demonstration that it is not the case that both the formula p and its negation ~p can derived in the system. But by whatever method one goes about it, all consistency proofs would seem to necessitate the primitive notion of contradiction; moreover, it seems as if this notion would simultaneously have to be "outside" the formal system in the definition of tautology.
When Emil Post in his 1930 Introduction to a general theory of elementary propositions extended his proof of the consistency of the propositional calculus (i.e. the logic) beyond that of Principia Mathematica (PM) he observed that with respect to a generalized set of postulates (i.e. axioms) he would no longer be able to automatically invoke the notion of "contradiction" -- such a notion might not be contained in the postulates:
- "The prime requisite of a set of postulates is that it be consistent. Since the ordinary notion of consistency involves that of contradiction, which again involves negation, and since this function does not appear in general as a primitive in [the generalized set of postulates] a new definition must be given". (Post 1930 Introduction to a general theory of elementary propositions in van Heijenoort 1967:272)
Post's solution to the problem is described in the demonstration An Example of a Successful Absolute Proof of Consistency offered by Nagel and Newman in their 1958 Gödel's Proof. They too observe a problem with respect to the notion of "contradiction" with its usual "truth values" of "truth" and "falsity". They observe that:
- "The property of being a tautology has been defined in notions of truth and falsity. Yet these notions obviously involve a reference to something outside the formula calculus. Therefore, the procedure mentioned in the text in effect offers an interpretation of the calculus, by supplying a model for the sytem. This being so, the authors have not done what they promised, namely, 'to define a propery of formulas in terms of purely structural features of the formulas themselves'. [Indeed] . . . proofs of consistency which are based on models, and which argue from the truth of axioms to their consistency, merely shift the problem." [boldface italics added, p. 109-110]
Given some "primitive formulas" such as PM's primitives S1 V S2 [inclusive OR], ~S (negation) one is forced to define the axioms in terms of these primitive notions. In a thorough manner Post demonstrates in PM, and defines (as do Nagel and Newman, see below), that the property of tautologous -- as yet to be defined -- is "inherited": if one begins with a set of tautologous axioms (postulates) and a deduction system that contains substitution and modus ponens then a consistent system will yield only tautologous formulas.
So what will be the definition of tautologous?
Nagel and Newman create two mutually exclusive and exhaustive classes K1 and K2 into which fall (the outcome of) the axioms when their variables e.g. S1 and S2 are assigned from these classes. This also applies to the primitive formulas. For example: "A formula having the form S1 V S2 is placed into class K2 if both S1 and S2 are in K2; otherwise it is placed in K1", and "A formula having the form ~S is placed in K2, if S is in K1; otherwise it is placed in K1" (pp. 110-111).
Nagel and Newman can now define the notion of tautologous: "a formula is a tautology if, and only if, it falls in the class K1 no matter in which of the two classes its elements are placed" (p. 111). Now the property of "being tauotologous" is described without reference to a model or an interpretation.
- For example, given a formula such as ~S1 V S2 and an assignment of K1 to S1 and K2 to S2 one can evaluate the formula and place its outcome in one or the other of the classes. The assignment of K1 to ~S1 places ~S1 in K2, and now we can see that our assignment causes the formula to fall into class K2. Thus by definition our formula is not a tautology.
Post observed that, if the system were inconsistent, a deduction in it (that is, the last formula in a sequence of formulas derived from the tautologies) could ultimately yield S itself. As as an assignment to variable S can come from either class K1 or K2, the deduction violates the inheritance characteristic of tautology, i.e. the derivation must yield an (evaluation of a formula) that will fall into class K1. From this, Post was able to derive the following definition of inconsistency without the use of the notion of contradiction:
- Definition. A system will be said to be inconsisent if it yields the assertion of the unmodified variable p [S in the Newman and Nagel examples].
In other words, the notion of "contradiction" can be dispensed when constructing a proof of consistency. More interestingly, an axiomatic system need not include the notion of "contradiction".
references:
- Jean van Heijenoort 1967 From Frege to Goedel: A Source Book in Mathematical Logic 1879-1931, Harvard University Press, Cambridge, MA, ISBN0-674-32449-8 (pbk.)
- Ernest Nagel and James R. Newman 1958 Gödel's Proof, New York University Press, Card Catalog Number: 58-5610.
Bill Wvbailey (talk) 16:13, 15 November 2009 (UTC)
bot and perp?[edit]
What does (or alternatively ) mean? Thanks, --Abdull (talk) 15:15, 22 December 2009 (UTC)
- In type theory (part of theoretical computer science) it means bottom type, which is why it's called \bot. In geometry, it means perpendicular, which is why it's called \perp. I'm not certain of the exact definition in formal logic, but I think it just means "a contradiction". That's not very helpful, though, if you were hoping to use to help you understand the rest of this article. --jholman (talk) 05:06, 11 November 2010 (UTC)
right-triangle proof[edit]
deleted, wrong section Jdl22 (talk) 05:43, 25 February 2010 (UTC)
Repaired vandalism from 2008[edit]
With this edit I have restored two sections that were removed without reason in early 2008, and not noticed until now. Could others please review the wording of Proof by contradiction and also whether the section "symbolic representation" could be better placed before the first use of the symbols. -84user (talk) 22:08, 17 March 2010 (UTC)
Clarification[edit]
I think the first sentence is a little confusing. It seems inadequate to say that 'contradiction' consists of 'logical incompatibility'. Certainly 'contradiction' does contain 'logical incompatibility', but contradiction is more than just logical incompatibility. A contradiction involves two propositions that both cannot be true and both cannot be false. A logical incompatibility is two propositions that both cannot be true but with no mention of both cannot be false (kind of like subcontraries on the square of opposition). This may seem nickpicking but the distinction must be maintained or else there is no difference between contradiction and incompatibility. Also, I think contradiction is only between two propositions, not 'two or more'.Thinkingbeingone (talk) 02:26, 20 October 2010 (UTC)
Conclusion?[edit]
I am not sure what is meant by 'conclusions' in the statement, "It occurs when the propositions, taken together, yield two conclusions..." Does this mean that the conclusion is the actual contradiction itself resulting from a proposition and its negation? Thinkingbeingone (talk) 19:18, 17 November 2010 (UTC)
Definition[edit]
I am suspicious about this definition being correct: "In classical logic, a contradiction consists of a logical incompatibility between two or more propositions."
I am not highly trained in classical logic so someone could help me. I was taught by my philosophy professor that a contradiction was a logical statement (TRUE or FALSE) that is always FALSE. A "logical incompatibility between two or more propositions" is only one type of a contradiction. Another type would be NOT(A OR NOT(A)), which is the inverse of a tautology. I realize that both are logically equivalent, but the current definition seems too specific. I would imagine that this is misleading to a reader who knows nothing about "classical logic."
Someone please correct this or me. —Preceding unsigned comment added by 75.84.211.112 (talk) 06:05, 18 November 2010 (UTC)
- A late response, but... you are quite correct. A contradiction does not need to consist of two or more propositions as the lede currently states. A single proposition can be a contradiction (self-contradictory) if it is false under all interpretations. For example, if we assume the law of identity, then ¬(a=a) is a contradiction. Dezaxa (talk) 05:19, 3 January 2021 (UTC)
- I think this is a matter of terminology changing over time. 'Negation of a tautology' is a simple definition that often serves the purposes of formal logic well, but 'a set of propositions whose conjunction is absurd' is more general (the former is an instance of a singleton such set) and is more in line with older sources. IIRC, Kant's Logic had contradiction explicitly defined in terms of a primitive notion of absurdity. In constructing derivations, we say we have a contradiction when we infer the negation of a premise or a previously established proposition; it's this sense of contradication we use in 'proof by contradiction'.
- The right thing to do is to assemble a set of well-sourced definitions, select an appropriately flexible one from these and document the others in a footnote. The list of rival definitions for the main Logic article grew so long that we started a spin-off article, Definitions of logic, to house them. This is hardly the most serious problem with the article as it stands, though. — Charles Stewart (talk) 12:48, 3 January 2021 (UTC)
Sloppy quasi syllogism[edit]
Certainly more and better could be done on the § on dialectical materialism. In syllogistic form the correct formulation would be A) the purpose of (any) society is the welfare of the members of that society; (B) modern society has extraordinary means to establish such "welfare"; (C) It does not - the resultant contradiction. Lycurgus (talk) 13:59, 14 May 2011 (UTC)
False premise in the illustration?[edit]
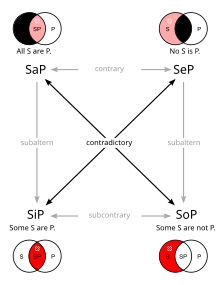
In the Venn diagrams, black areas are empty and red areas are nonempty.
The faded arrows and faded red areas apply in traditional logic.
A first impression, of a external reader, about illustration: "All S are P" = "all x of S is also an element of P", must be represented by "S⊂P"... Not seems didactic. Somebody can explain here? I am wrong in my "first and fast view"? --Krauss (talk) 11:04, 28 August 2014 (UTC)
- I find the "Venn drawings" confusing (the ones with black and pink are not true Venn drawings), but I think they are "correct" if we allow for "an interpretation". I've added to the caption the words from the "square of opposition" page; these words may help. The black moon-shaped space is empty of elements, so all of the elements of the pink SP are inside the white circle P, thus SP is a proper subset of P (again: this and the drawing to the right are not true Venn drawings. The one on the left should have the SP circle entirely inside the P circle, and the one on the right should have have an S-circle completely outside the P circle ). BillWvbailey (talk) 22:18, 28 August 2014 (UTC)
simple example?[edit]
Would it be possible to have a real-world example, or is this purely a theory topic? For instance, isn't the liar paradox a contradiction? 92.23.191.106 (talk) 12:09, 3 April 2017 (UTC)





